Question

Complete the equation of the line through (6,-6) and (8,8)

Answer 1

General formula to determine the equation of the line
y - y₁ = m(x - x₁)
(x₁,y₁) is one of the points which lies n the line
m represents the slope

Find the slope
Given:
(x₁,y₁) = (6,-6)
(x₂,y₂) = (8,8)

We could find the slope by using this formula
m =
`( y_(2) -y_(1) )/( x_(2) -x_(1) )`

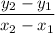
Plug in the numbers
m =
`( y_(2) -y_(1) )/( x_(2) -x_(1) )`
m =
`(8-(-6))/(8-6)`
m =
`(14)/( 2 )`
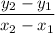
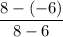
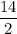
m = 7
The slope is 7

Determine the line equation
Plug one of the points (you could choose any of points given from the question) and the slope to the formula of line equation
y - y₁ = m(x - x₁)
y - (-6) = 7(x - 6)
y + 6 = 7x - 42
y = 7x - 42 - 6
y = 7x - 48
This is the equation of the line