Question

A rectangle has a perimeter of 30 feet and an area of 50 square feet. What are the dimensions of the rectangle?

A) 2 feet, and 15 feet
B) 2 feet, and 25 feet
C) 4 feet, and 11 feet
D) 5 feet, and 10 feet

Answer 1

perimeter (p) = 2×length (l) + 2×width (w)
p = 2l+2w
area (a) = l×w, so solve for one (I'll use l):

`a = l * w \\ l = a / w \\ p = 2l + 2w = 2(l + w)`
since p = 30, and a = 50, substitute the "a÷w" in for l in the perimeter equation:

`p = 2(l + w) = 2((a / w) + w) \\ = 2((a / w) + ( {w}^(2) / w)) \\ p= 2((a + {w}^(2)) / w`
Now plug in p and a values:

`p= 2((a + {w}^(2)) / w) \\ 30 = 2((50 + {w}^(2)) / w) \\ 30 / 2 = (50 + {w}^(2)) / w \\ 15w = 50 + {w}^(2)`

`15w = 50 + {w}^(2) \\ {w}^(2) - 15w + 50 = 0 \\ (w - 5)(w - 10) = 0`
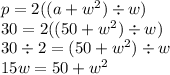
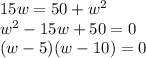
therefore width can be either 5 or 10 (but not both), so let's plug in:
l = a÷w = 50÷5 = 10
So if w = 5, then l = 10

D) 5 feet, and 10 feet