Answer:
f(x) is shifted 4 units down from the graph g(x).
Explanation:
Given :
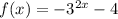
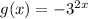
To Find: How does the graph of
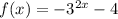 differ from the graph of
differ from the graph of
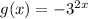 ?
?
Solution:
Rule : f(x)→f(x)-b
So, The graph f(x) is shifted down by b units
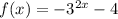
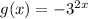
On comparing we can say g(x) needs to shift 4 units down to reach f(x)
Using Rule we can say that f(x) is shifted 4 units down from the graph g(x).
So, Option C is correct.
f(x) is shifted 4 units down from the graph g(x).