Question

If someone could help me with number 26...

Answer 1

Given:

`\text{sec x} - \sqrt{\text{2 sec x}-1} =0`

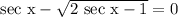Solution:
To solve the equation, it would be best if we remove the root. We remove the root by squaring the equation, but first we need to move the root and the content to the left side.

`\text{sec x} - \sqrt{\text{2 sec x}-1} =0`

`\text{sec x} = \sqrt{\text{2 sec x}-1}`

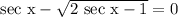
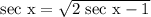
Then square both side to remove the root

`\text{sec}^2 x= \text{2 sec x}-1`

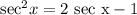
After removing the root, move all terms to the left side
sec² x - 2 sec x + 1 = 0

Do factorization, remember that
a² - 2a + 1 = (a - 1)²
So,
sec² x - 2 sec x + 1 = 0
(sec x - 1)² = 0
sec x - 1 = 0
sec x = 1

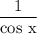
`\frac{1}{\text{cos x}}` = 1
cos x = 1
cos x = cos 0°
x = 0°