Question

1. simplify and write in standard form. then, classify the polynomial by degree and number of terms.

(5x^3 + 3x^2 - 7x + 10) - (3x^3 - x2 + 4x - 1)

is it 2x^3+4x^2-11x+11

Answer 1

Yes, the answer is 2x^3+4x^2-11+11

Answer 2

The Standard form of a polynomial is in the form of:

`a_nx^n+a_(n-1)x^(n-1)+.....+a_2x^2+a_1x+a_0`

i.e, the highest exponent goes first until the last term with the lowest exponent.

Degree of a polynomial is the highest exponent, and the coefficient of this term is the leading coefficient. The constant term is the one without an x variable.

Simplify:
`(5x^3 + 3x^2 - 7x + 10) - (3x^3 - x^2 + 4x - 1)`

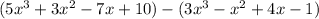
Remove the parentheses we get;

`5x^3 + 3x^2 - 7x + 10 - 3x^3 + x^2 - 4x + 1`

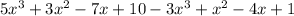
Combine like terms, we get;

`2x^3 + 4x^2 - 11x + 11`

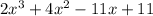
Standard form of a polynomial =
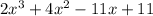`2x^3 + 4x^2 - 11x + 11` [descending exponent ]

Degree of a polynomial(i.,e highest exponent is from
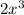`2x^3`) is, 3

Number of terms = 4 .