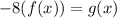Question

How is the function f(x)=-1/2sin5x related to the function g(x)=4sin5x?

Answer 1

Hence, the required relationship is:
`-8(f(x))=g(x)`

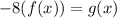
Explanation:

We have been given two functions:

`f(x)=-(1)/(2)sin 5x`

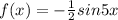
And
`g(x)=4sin 5x`

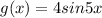
We can see that angle is same that is sin 5x

So, for a relationship between both the functions we need to relate the amplitude that is
`y=a sinbt` (1)

Where, a is amplitude.

If we compare two functions with (1) amplitude of f(x) is -1/2 and g(x) is 4

So, if we multiply -8 with f(x) that is:

`-8(f(x))=-8(-(1)/(2)sin 5x)`

`\Rightarrow -8(f(x))=4sin 5x`

`\Rightarrow -8(f(x))=g(x)`

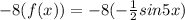
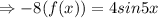
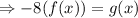
Hence, the required relationship is:
`-8(f(x))=g(x)`

Answer 2

From the question we have that f(x) = -1/2 sin 5x and g(x) = 4 sin5x
Let's try to calculate -8f(x)
- 8f(x) = -8 (-1/2 sin 5x)
This becomes 4sin 5x
Since the function g(x) is -8 times f(x)
Hence g(x) = -8f(x)