Question

(TEN POINTS)

Write a linear function f with the values f(−1)=−3 and f(2)=6.
A function is f(x)=
(please put answer in form of y=mx+b)

Answer 1

f(-1)= -3 is (-1,-3) and f(2) = 6 is (2,6) where f(x) = y
y=mx + b is the slope-intercept form whereas m equals the slope (rate of change) and b equals the y-intercept (initial amount/what y is when x is 0.)

First, we need to find the slope between the two points (-1,-3) and (2,6). To find the slope we could use one of it's formulas
`(y^2 - y^1)/(x^2 - x^1)`.
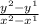
1. (-1,-3)
2. (2,6)

`(6 - -3)/(2 - -1)` →
`(9)/(3)` →
`(3)/(1)`

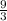
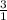
The slope is 3 (
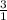
`(3)/(1)`). Thusly, y = 3x + b

To find out the y-intercept, we can reverse the slope. [Note: This
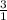
`(3)/(1)` is in
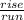
`(rise)/(run)` where rise is 'y' and run is 'x'. Reversed would be
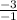
`(-3)/(-1)` ]. Take the second ordered pair and use our reversed slope on it until we get 0 for x.

(2, 6) ⇒ (2 - 1, 6 -3) ⇒ (1, 3) ⇒ (0,0)

Y-intercept is 0. Therefore, y= 3x + 0 [NOTE: y = f(x), so if you want it in function notation form it's just f(x) = 3x + 0.]