Hey. Let me help you on this one.
In this question, we have two hexagons which are similar; however, their size is different.
Our main focus here are not the hexagons, though. All we will be paying attention here to is one side of a hexagon which is 25 units of length. We don't know the length of the corresponding side in another hexagon; however, we do know the size ratio.
The 25-units side is portrayed by a five in the 5:2 ratio. First step we should take is to simplify the ratio, and possibly try getting the denominator down to 1.
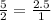
Now that we have this ratio, we know that 25-units side is 2.5 times bigger than the side we are looking for. All that we have to do now is set up an equation that we can then solve.
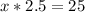
In this equation, we will be finding a number that's 2.5 times less than 25. If "x" is multiplied by 2.5, the product will be 25.
Let's divide both sides by 2.5 since we need to get 2.5 away from x.
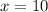
Awesome. Equation is solved, and now that we know what is "x", we can be sure that this is the final answer. I will be attaching an image showing you what exactly I did with the equation in case you are still confused.
Answer: The corresponding side of the hexagon is 10 units.