Question

What is the value of x? Triangle V T K with segment T Y such that Y is on segment V K, between V and K. Angle V T Y is congruent to angle Y T K. V T equals 57 millimeters, V K equals x, Y K equals 68 millimeters, and T K equals 129.2 millimeters.

Answer 1

98

Step-by-step explanation:

Confirming that this answer is correct! :)

Answer 2

Answer: 98 millimeters

Step-by-step explanation:

Since angle VTY is congruent to angle VTK, segment TY bisects angle VTK. Since Y is on segment VK, between V and K, we can use the Angle Bisector Theorem, which states that


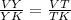
`(VY)/(YK) = (VT)/(TK)` (1)

Since x= VK = VY + YK, we need to obtain VY since YK = 68.

VY is obtained by multiplying the denominator YK on both sides of equation (1). So,


`VY = ((VY)(VT))/(TK) = ((68)(57))/(129.2) \\ewline VY = 30`

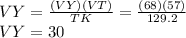
Hence,

x = VK = VY + YK
x = 30 + 68
x = 98 millimeters