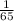Question

A card is drawn from a standard deck and a letter is chosen from the word incredible . What is the probability of drawing a king then getting an I

Answer 1

A deck as 52 cards and 4 kings
p(king) = 4/52 =1/13

[Getting l as in the letter “L” and not the letter “i” right?]

P(l) = 1/10

P(king and I) = 1/13 x 1/10 = 1/130

Answer 2

The probability of drawing a king then getting an I is
`(1)/(65)`

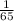
Explanation:

Topic: Independent Probability

Given:

• Standard deck of cards
• The word, incredible

There are 52 cards in a deck, out of which 4 are kings.

Let n(C) represents the number of cards and n(K) represents the number of Kings

n(C) = 52

n(K) = 4

The probability of getting a king is calculated as follows;

Let P(K) represents the probability of getting a king

`P(K) = (n(K))/(n(C))`; By Substitution, we have

`P(K) = (4)/(52)`

`P(K) = (1)/(13)`

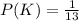
There are 10 letters in the word incredible, out of which 2 are letter i.

Let n(W) represents the number of letters and n(I) represents the number of letter i

n(W) = 10

n(I) = 2

The probability of getting a letter i is calculated as follows;

Let P(I) represents the probability of getting a letter i

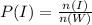`P(I) = (n(I))/(n(W))`; By Substitution, we have

`P(K) = (2)/(10)`

`P(K) = (1)/(5)`

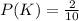
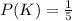
The two events above are independent. Two events are said to be independent if the incidence of one event does not affect the probability of the other event.

So, the probability of drawing a king then getting an I is represented as
`P(K n I)` and it's calculated as follows;

`P(K n I) = P(K) * P(I)`

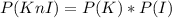
By Substitution

`P(K n I) = (1)/(13) * (1)/(5)`

`P(K n I) = (1)/(65)`

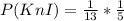
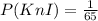
Hence, the probability of drawing a king then getting an I is
`(1)/(65)`