Answer:
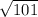 feet or 10.05 feet.
feet or 10.05 feet.
Explanation:
We know that wall stands vertical to the ground makes right angle.
Then, the triangle made by ladder must be right triangle.
Now, by Pythagoras theorem of right triangle we have,
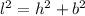 , where h is the height of the wall , l is length of ladder and b is the distance of bottom from the building.
, where h is the height of the wall , l is length of ladder and b is the distance of bottom from the building.
By considering the given information, we have
![(51)^2=(50)^2+b^2\\\\\Rightarrow\ b^2=(51)^2-(50)^2\\\\\Rightarrow\ b^2=2601-2500=101\\\\\Rightarrow\ b=√(101)=10.0498756211\approx10.05\ \text{[ Rounded to the nearest two decimal places. ]}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/6hfy49f4y3djfv6x3w9n1x7or9qm8p54o0.png)
Hence, the distance of bottom from the building = 10.05 feet.