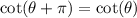Answer:
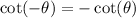
and
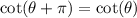
Explanation:
Justin wants to evaluate
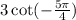 .
.
First he can use the fact that, the cotangent function is an odd function and write.
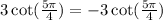 .
.
Also the cotangent function is positive in both the first and third quadrant, so we can use the symmetric property;
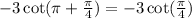 .
.
Hence the correct answers are;
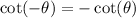
and