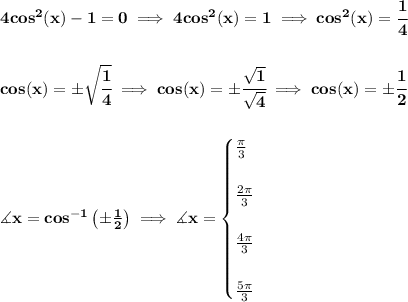Question

Find all solutions of the equation on the interval [0,2π]

1) 3 tan x -√3 =0

2) 4 cos² x - 1 = 0

Answer 1

1)


`\bf 3tan(x)-√(3)=0\implies 3tan(x)=√(3)\implies \boxed{tan(x)=\cfrac{√(3)}{3}}`

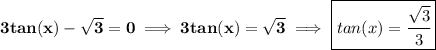
now, let's take a peek at your Unit Circle, as you should have one, if you don't, this is a prime time to get one, you'll need it, you can find many online, or I can post one here for you, many good ones. Anyhow, let's take a peek at π/6.


`\bf \cfrac{\pi }{6}\quad \begin{cases} sine=&(1)/(2)\\ cosine=&(√(3))/(2) \end{cases}\qquad tan\left( (\pi )/(6)\right)=\cfrac{sin\left( (\pi )/(6)\right)}{cos\left( (\pi )/(6)\right)}\implies \cfrac{(1)/(2)}{(√(3))/(2)}`


`\bf \cfrac{1}{2}\cdot \cfrac{2}{√(3)}\implies \cfrac{1}{√(3)}\impliedby \textit{now, let's \underline{rationalize the denominator}} \\\\\\ \cfrac{1}{√(3)}\cdot \cfrac{√(3)}{√(3)}\implies \cfrac{1√(3)}{(√(3))^2}\implies \boxed{\cfrac{√(3)}{3}}`

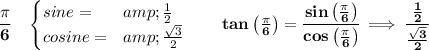
now, the tangent function is positive, if both the numerator and denominator have the same sign, that happens in the I Quadrant, as in π/6, but is also true in the III Quadrant, since both are negative.


`\bf \measuredangle x= \begin{cases} (\pi )/(6)&I~Quadrant\\\\ (7\pi )/(6)&III~Quadrant \end{cases}`



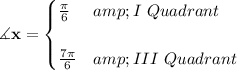
2)


`\bf 4cos^2(x)-1=0\implies 4cos^2(x)=1\implies cos^2(x)=\cfrac{1}{4} \\\\\\ cos(x)=\pm\sqrt{\cfrac{1}{4}}\implies cos(x)=\pm\cfrac{√(1)}{√(4)}\implies cos(x)=\pm\cfrac{1}{2} \\\\\\ \measuredangle x=cos^(-1)\left( \pm(1)/(2) \right)\implies \measuredangle x= \begin{cases} (\pi )/(3)\\\\ (2\pi )/(3)\\\\ (4\pi )/(3)\\\\ (5\pi )/(3) \end{cases}`