Question

Please help
thank you

Answer 1

Question 1:

Use the Pythagorean theorem.

If
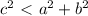
`c^2\ \textless \ a^2+b^2`, then the angle is acute.
If
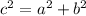
`c^2=a^2+b^2`, then the angle is right.
If
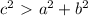
`c^2\ \textgreater \ a^2+b^2`, then the angle is obtuse.


`a=18`

`b=80`

`c=81`


`c^2=6561`

`a^2+b^2=324+6400=6724`


`\boxed {c^2\ \textless \ a^2+b^2}`

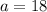
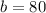
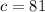
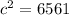
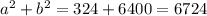
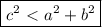
Thus, the angle is acute.

Question 2:

Take the square root of the area to get the side length.


`√(200) = √(100*2) =10 √(2)`

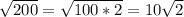
That's the side length. Since we have a 45-45-90 right triangle if we divide the square across its diagonal, we just multiply the side length by the square root of 2 in order to get the diagonal length.


`10 √(2) * √(2)`

`=20`

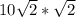
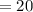
Your answer is 20 m. Hope this helps! :)