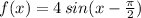Answer:
Option A is correct.i.e,
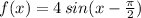
Explanation:
We are given with a graph .
A points from graph which satisfies it =
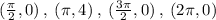
We check which equation satisfy points.
Option A:
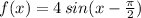
Let,
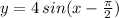
we have
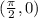
LHS = y = 0
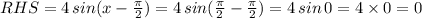
LHS = RHS
Thus, This Option is correct.
Option B:
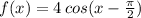
Let,
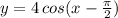
we have
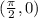
LHS = y = 0
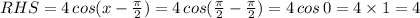
LHS ≠ RHS
Thus, This Option is not correct.
Option C:
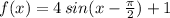
Let,

we have
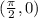
LHS = y = 0

LHS ≠ RHS
Thus, This Option is not correct.
Option D:
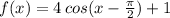
Let,
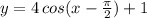
we have
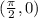
LHS = y = 0

LHS ≠ RHS
Thus, This Option is not correct.
Therefore, Option A is correct.i.e,