Question

What is the value of x given that pq||bc?

Answer 1

Hey there! :D

In the triangle, you can see that BA has lengths 12 and 6.

Well, 6 is half of 12.

So,

26/2= 13

x=13

The sides are proportional, so the same factor works for both sides.

I hope this helps!
~kaikers

Answer 2

x = 13 units

Explanation:

Given that : PQ ║ BC

To find : The value of x

Solution :

In ΔAPQ and ΔABC

∠APQ = ∠ABC ( Corresponding angles are always equal)

∠AQP = ∠ACB (Corresponding angles are always equal)

So, By AA similarity postulate of triangles, ΔAPQ ~ ΔABC

Since, The sides of the similar triangles are proportional to each other

`\implies(AP)/(AB)=(AQ)/(AC)\\\\\implies(6)/(12+6)=(x)/(26+x)\\\\\implies 18x=26* 6+6x\\\\\implies 12x=26* 6\\\\\implies\bf x = 13`

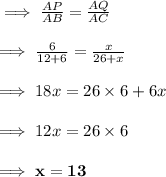
Hence, AQ = 13 units