Question 1:In this 45-45-90 right triangle, the hypotenuse has a length of
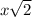
and the leg has a length of

We want to solve for x. Let's start with the equation of
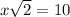
and solve for x.
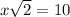
Divide both sides by the square root of 2.
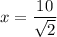
Simplify the fraction by multiply both the numerator and denominator by the sqaure root of 2.
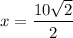
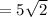 Question 2:
Question 2:Let's imagine a right triangle where the legs are 250 and we want to solve for the hypotenuse. Since the legs are congruent, this is a 45-45-90 right triangle.
Multiply 250 by the square root of 2 and use a calculator.
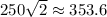
Hope this helps! :)