Answer:
![[C]_(eq)=4(0.733M)=2.932M](https://img.qammunity.org/2019/formulas/chemistry/college/xl9d56bztlv686nu4izth1i2hv2swg0uuy.png)
![[A]_(eq)=2.20M-3(0.733M)=0.001M](https://img.qammunity.org/2019/formulas/chemistry/college/on7uxw2rg5l64zld82fcaw218ljph9gtce.png)
![[B]_(eq)=3.70M-2(0.733M)=2.23M](https://img.qammunity.org/2019/formulas/chemistry/college/97bk6suwnux91nyi5hzlt7i37z772x4bo9.png)
Step-by-step explanation:
Hello,
In this case, probably, the undergoing chemical reaction is:
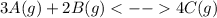
Nonetheless, the equilibrium constant is not given, but could be assumed, therefore, let me assume it is 1.13x10¹⁹ (very close to a constant I found for a similar exercise on the Ethernet), thus, the initial concentrations of A and B are computed below based on the given moles and the container volume:
![[A]_0=(2.20mol)/(1.00L) =2.20M](https://img.qammunity.org/2019/formulas/chemistry/college/njie20kb6zd6gsf6okx6cr3xo4486g0h05.png)
![[B]_0=(3.70mol)/(1.00L) =3.70M](https://img.qammunity.org/2019/formulas/chemistry/college/qlbhsw8m40m81522yzoydzppue1jh588mf.png)
In such a way, by applying the law of mass action in addition to the ICE table, the equilibrium statement turn out into:
![Kc=([C]_(eq)^4)/([A]_(eq)^3[B]_(eq)^2)](https://img.qammunity.org/2019/formulas/chemistry/college/7h62z3fhhv079ywvkja2mon7v2vjjg0uy5.png)
Now, by inserting the initial concentrations of both A and B and the reaction change,
 , one obtains:
, one obtains:

Such equation is a highly non-lineal one, that is why we must apply a method such as Newton-Raphson to compute the roots which define the value of the change
 , thus, after applying it, the roots are:
, thus, after applying it, the roots are:
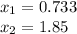
The valid root is
 as the other one produces a negative concentration of A at equilibrium, therefore, the requested concentration turn out into:
as the other one produces a negative concentration of A at equilibrium, therefore, the requested concentration turn out into:
![[C]_(eq)=4(0.733M)=2.932M](https://img.qammunity.org/2019/formulas/chemistry/college/xl9d56bztlv686nu4izth1i2hv2swg0uuy.png)
![[A]_(eq)=2.20M-3(0.733M)=0.001M](https://img.qammunity.org/2019/formulas/chemistry/college/on7uxw2rg5l64zld82fcaw218ljph9gtce.png)
![[B]_(eq)=3.70M-2(0.733M)=2.23M](https://img.qammunity.org/2019/formulas/chemistry/college/97bk6suwnux91nyi5hzlt7i37z772x4bo9.png)
However, you can just modify Kc if is different to the one I assumed and perform the Newton-Raphson method to compute the adequate root.
Best regards.