Question

The mean income of a group of sample observations is $500; the standard deviation is $40. according to chebyshev's theorem, at least what percent of the incomes will lie between $400 and $600?

Answer 1

Answer: 84%

Step-by-step explanation:

Let

x = any income in the sample observation

`\mu` = mean = $500

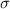
`\sigma` = standard deviation = $40
k = any positive numbers

Chebyshev's theorem states that at least (1 - 1/k²) of the incomes is within k standard deviations from the mean.

In terms of mathematical equation:


`P(|x - \mu| \leq k\sigma) \geq 1 - (1)/(k^2)`

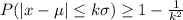
To use Chebyshev's theorem, we get the expressions for


`|x - \mu| = |x - 500|`

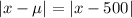
Since we are concerned with the incomes between $400 and $600,


`400 \leq x \leq 600 \\ewline \Leftrightarrow -100 \leq x - 500 \leq 100 \\ewline \Leftrightarrow |x - 500| \leq 100 \\ewline \Leftrightarrow |x - 500| \leq 2.5(40)`

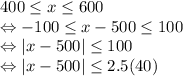
Thus, we take k = 2.5. By Chebyshev's theorem,


`P(|x - \mu| \leq k\sigma) \geq 1 - (1)/(k^2) \\ewline P(|x - 500| \leq 2.5(40)) \geq 1 - (1)/(2.5^2) \\ewline P(|x - 500| \leq 100) \geq 1 - 0.16 \\ewline P(-100 \leq x - 500 \leq 100) \geq 0.84 \\ewline \boxed{P(400 \leq x \leq 600) \geq 0.84}`

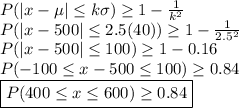
Therefore, at least 84% of the incomes will lie between $400 and $600.