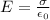Question

What is the electric field strength just outside the flat surface of the conductor?

Answer 1

We can find the answer step-by-step:

1) The electric charges on a conductor must lie entirely on its surface. This is because the charges have same sign, so the force acting between each other is repulsive therefore the charges must be as far apart as possible, i.e. on the surface of the conductor.

2) We consider a cylinder perpendicular to the surface of the conductor, that crosses the surface with its section. We then apply Gauss law, which states that the flux of the electric field through this cylinder is equal to the total charge inside it divided the electrical permittivity:

`\Phi = (Q)/(\epsilon_0)`

3) The electric field outside the surface is perpendicular to the surface itself (otherwise there would be a component of the electric force parallel to the surface, which would move the charge, violating the condition of equilibrium). The electric field inside the conductor is instead zero, because otherwise charges would move violating again equilibrium condition. Therefore, the only flux is the one crossing the section A of the cylinder outside the surface:

`\Phi = E A`

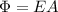
4) The total charge contained in the cylinder is the product between the section, A, and the charge density
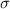
`\sigma` on the surface of the conductor:

`Q=\sigma A`

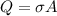
5) Substituting the flux and the charge density inside Gauss law, we can find the electric field just outside the surface of the conductor:

`EA= (\sigma A)/(\epsilon_0)`
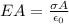
therefore

`E= (\sigma)/(\epsilon_0)`