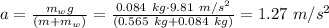Question

Harry and ron set up this experiment with a glider, whose mass they have measured to be 565 g, and seven washers hanging from the string. if each washer has a mass of 12 g, what is the acceleration of the system, in m/s2

Answer 1

Let's call
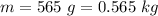
`m=565~g=0.565~kg` the mass of the glider and
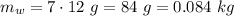
`m_w=7\cdot12~g =84~g=0.084~kg` the total mass of the seven washers hanging from the string.
The net force on the system is given by the weight of the hanging washers:

`F_(net) = m_w g`
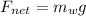
For Newton's second law, this net force is equal to the product between the total mass of the system (which is
`m+m_w`) and the acceleration a:

`F_(net)=(m+m_w)a`
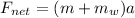
So, if we equalize the two equations, we get

`m_w g = (m+m_w)a`
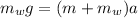
and from this we can find the acceleration:

`a= (m_w g)/((m+m_w)) = (0.084~kg \cdot 9.81~m/s^2)/((0.565~kg+0.084~kg))=1.27~m/s^2`