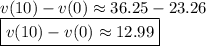Question

An object undergoes acceleration of 2.3i^+3.6j^m/s2 over a 10-s interval. at the end of this time, its velocity is 33i^+15j^m/s. by how much did its speed change

Answer 1

Answer: 12.99 m/s

Step-by-step explanation:

Since the acceleration is constant, we can use the following formula for the velocity


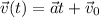
`\vec{v}(t) = \vec{a}t + \vec{v}_0` (1)

Where:


`\vec{v}(t) = \text{velocity at time }t \\ewline \indent \vec{a} = \text{acceleration at time }t \\ewline \indent \vec{v}_0 = \text{initial velocity, i.e., velocity at }t=0`

Since at t = 10 s,


`\vec{v}(10) = 33\textbf{i} + 15\textbf{j} \\ewline \indent \vec{a} = 2.3\textbf{i} + 3.6\textbf{j}`

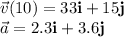
the unknown variable in equation (1) is
`\vec{v}_0`.

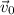
At t = 10 s, equation 1 becomes:


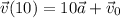
`\vec{v}(10) = 10\vec{a} + \vec{v}_0` (2)

By subtracting both sides of equation (2) by
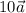
`10\vec{a}`, we have


`\vec{v}_0 = \vec{v}(10) - 10\vec{a} \\ewline \vec{v}_0 = 33\textbf{i} + 15\textbf{j} - 10(2.3\textbf{i} + 3.6\textbf{j}) \\ewline \vec{v}_0 = 33\textbf{i} + 15\textbf{j} - (23\textbf{i} + 36\textbf{j}) \\ewline \boxed{\vec{v}_0 = 10\textbf{i} - 21\textbf{j}}`

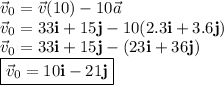
Now, we let

v(10) = speed of the object at t = 10
v(0) = speed of the object at t = 0

Recall that speed is the magnitude of the velocity and so


`v(10) = |\vec{v}(10)| \\ewline \indent \indent = |33\textbf{i} + 15\textbf{j}| \\ewline \indent \indent = √(33^2 + 15^2) \\ewline \indent \boxed{v(10) \approx 36.25} \\ewline \\ewline \indent v(0) = |\vec{v}(0)| \\ewline \indent \indent = |10\textbf{i} - 21\textbf{j}| \\ewline \indent \indent = √(10^2 + (-21)^2) \\ewline \indent \boxed{v(0) \approx 23.26}`

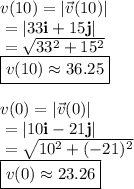
Hence, the change of speed after 10 s is given by


`v(10) - v(0) \approx 36.25 - 23.26 \\ewline \indent \boxed{v(10) - v(0) \approx 12.99}`