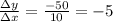Question

Find the average rate of change of k(x)=5x–19 over the interval [

-
14,
-
4].

Answer 1

The rate of change of a function can be modeled with the following expression:




Where Δx is the change in x value, and Δk(x) is the corresponding change in k(x). We're given the two extremes of x, so we can calculate the change in x to be


`\Delta{x}=-4-(-14)=10`

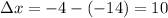
To find the change in k(x), we can calculate the values of k(x) at x = -14 and x = -4 and find the difference between them:


`k(-14)=5(-14)-19=-70-19=-89\\ k(-4)=5(-4)-19=-20-19=-39\\ \Delta{y}=k(-14)-k(-4)=-89-(-39)=-50`

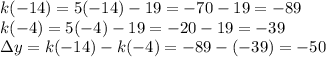
So, the rate of change for the function from x = -14 to x = -4 is


`\frac{\Delta{y}}{\Delta{x}}= (-50)/(10)=-5`