Question

80% of the items produced are non-defective. if three items are examined, what is the probability that at most one is non- defective? use the binomial probability function to answer this question.

Answer 1

Binomial distribution can be used because the situation satisfies all the following conditions:
1. Number of trials is known and remains constant (n)
2. Each trial is Bernoulli (i.e. exactly two possible outcomes) (success/failure)
3. Probability is known and remains constant throughout the trials (p)
4. All trials are random and independent of the others
The number of successes, x, is then given by

`P(x)=C(n,x)p^x(1-p)^(n-x)`
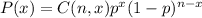
where

`C(n,x)=(n!)/(x!(n-x)!)`

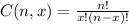
Here given
p=0.8 (success=non-defective)
n=3
x=0 or 1
Then

`P(0)+P(1)`

`=\sum_(x=0)^1C(n,x)p^x(1-p)^(n-x)`

`=C(3,0)0.8^0(1-0.8)^(3-0)+C(3,1)0.8^1(1-0.8)^(3-1)`

`=1(1)0.08+3(0.8)(0.04)`

`=0.08+0.096`

`=0.104`

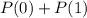
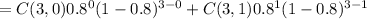
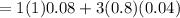
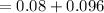
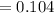
Answer: probability of at most one non-defective out of a random sample of three is 0.104

Answer 2

The probability that produced item is non-defective is
`p=0.8` and the probability that produced item is defective is
`q=1-p=1-0.8=0.2.`

1. Find the probability all produced items are defective:

`Pr_1=q^3=(0.2)^3=0.008.`

2. Find the probability that one produced item is non-defective and 2 are defective:

`Pr_2=C_3^1p^1q^2=(3!)/(1!(3-1)!)\cdot 0.8\cdot (0.2)^2=(2\cdot 3)/(2)\cdot 0.8\cdot 0.04=3\cdot 0.032=0.096.`

3. The probability that at most one produced is non- defective is

`Pr=Pr_1+Pr_2=0.008+0.096=0.104.`

Answer: 0.104.