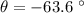Question

A ball is shot from the ground into the air. at a height of 8.9 m, its velocity is v overscript right-arrow endscripts equals 7.6 i overscript Ì endscripts plus 7.4 j overscript Ì endscripts ⢠m divided by s, with i overscript Ì endscripts horizontal and j overscript Ì endscripts upward. (a) to what maximum height does the ball rise? (b) what total horizontal distance does the ball travel? what are the (c) magnitude and (d) angle (below the horizontal; give as negative) of the ball's velocity just before it hits the ground?

Answer 1

Let's rewrite the velocity at a height h of 8.9 m as:

`v_x = 7.6~m/s`

`v_(yh) = 7.4~m/s`
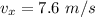
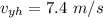
The motion of the ball is a parabolic motion: it is a uniform motion on x-axis (so,
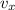
`v_x` is constant) and an accelerated motion on the y-axis (with acceleration equal to
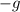
`-g`, the gravitational acceleration, with a negative sign because it points downwards).

Let's solve the exercise step-by-step.

a) We can solve this part by writing the laws of motion on x and y using the data at h=8.9 m as initial data.

`S_x(t)=v_x t`

`S_y(t)=h+v_(yh)t- (1)/(2)gt^2`

`v_y(t) = v_(yh)-gt`

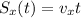
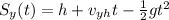
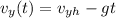
The maximum height
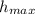
`h_(max)` is the height at which the velocity on the y-axis is zero. We can find the time
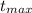
`t_(max)` at which this happens by requiring
`v_y(t_(max))=0`:

`0=v_(yh)-gt_(max)`
from which we find

`t_(max)= (v_y)/(g) = (7.4~m/s)/(9.81~m/s^2)=0.75~s`
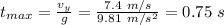
and then substituting in
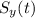
`S_y(t)` we find the maximum height:

`S_y(t_(max))=h_(max)= 8.9~m+7.4~m/s \cdot 0.75~s-(1)/(2) 9.81~m/s^2 \cdot (0.75~s)^2=`

`=11.7~m`

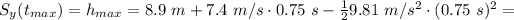
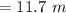
2) To find the total horizontal distance, we must find the intial conditions of the motion, at t=0. Let's call
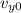
`v_(y0)` the initial velocity on the y-axis (we already know the initial velocity on the x-axis, which is
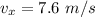
`v_x=7.6~m/s`. Then the velocity law on the y-axis is

`v_y(t) = v_(y0)-gt`
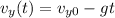
let's also call
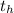
`t_h` the time t at which the ball reaches the height h=8.9m. At this time
`t_h`,
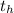
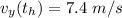
`v_y(t_h)=7.4~m/s`. Therefore we can write the following system of equations:

`S_y(t_h) = 8.9~m = v_(y0)t_h - (1)/(2) 9.81 t_h^2`

`v_y(t_h) = 7.4 = v_(y0)-9.81 t_h`
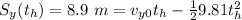
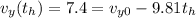
Solving this system, we find

`t_h=0.79~s`
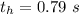
and

`v_(y0)=15.1~m/s`
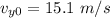
now that we know the initial velocities on both axis, we can find the time
`t_0` at which the ball reaches the ground. This happens when
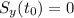
`S_y(t_0)=0`. The law of motion on y is

`S_y(t)=v_(y0) t - (1)/(2) g t^2`
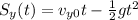
And if we require
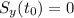
`S_y(t_0)=0`, we find two solutions: t=0 (beginning of the motion) and
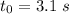
`t_0=3.1~s`, which is the moment when the ball reaches the ground. To find the total horizontal distance covered we just need to put this time into the equation of
`S_x(t)`:

`S_x(t_h)=v_x t_h = 23.4~m`

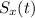
c) To solve this part of the problem, we must find the vertical velocity at the time the ball hits the ground, so:

`v_y(t_h)=v_(y0)-gt_h=15.1~m/s-9.81~m/s^2\cdot3.1~s=-15.3~m/s`
which is negative because now the ball is going downwards.
So, the magnitude of the velocity just before the ball hits the ground is

`v= √(v_x^2+v_y^2)= √((7.6~m/s)^2+(-15.3~m/s)^2) = 17.1~m/s`

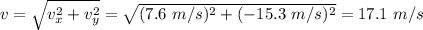
d) The tangent of the angle of the velocity is the ratio between the two components of the velocity:

`tg \theta = (v_x)/(v_y) = (-15.3~m/s)/(7.6~m/s)`
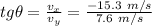
from which we find

`\theta = -63.6~^(\circ)`

Answer 2

The first thing we must do is write the kinematic equations for each component.
For vertical component:
Speed:
Vy = Vyi-g * t
Vyi -9.8 * t1 = 7.4
Vyi = 7.4 + 9.8 * t
Height:
y = Vyi * t- (1/2) * g * t ^ 2
7.4 * t + 9.8 * t ^ 2-4.9 * t ^ 2 = 8.9
4.9t ^ 2 + 7.4 * t-8.9 = 0
The roots are
t1 = 0.789729866757189 s
t2 = -2.299933948389842 s
Positive time, therefore:
t = 0.79 s
Then, the initial vertical velocity is:
Vyi = 7.4 + 9.8 * t
Vyi = 7.4 + 9.8 * (0.79)
Vyi = 15,142 m / s
For the maximum height we have that the final velocity is zero in the vertical component
Vy = Vyi-g * t = 0
t = Vyi / g
t = 15,142 / 9.81
t = 1.543 s
Then, the maximum height will be:
y (1,543) = (15,142) * (1,543) - (1/2) * (9.81) * (1,543) ^ 2
y = 11.68 m
The flight time is:
tv = 2 * t
tv = 2 * (1,543)
tv = 3.086 s

Then, the horizontal distance traveled is:
x = Vix * tv
x = (7.6) * (3.086)
x = 23.4536 m

After reaching the maximum height the ball falls with gravity:
11.68 = (1/2) * (9.8) * t ^ 2
Clearing t:
t = ((11.68 * 2) / (9.8)) ^ (1/2)
t = 1.543 s (Therefore, as mentioned above, tv = 2 * t)
Then,
Vyf = g * t = -9.8 * (1,543) = -15.1214
Then, Vyf = Vyi = -15.1214 m / s
Vxi = Vxf = Vx = 7.6 m / s
THE magnitude of the speed is:
v = sqrt (7.6 ^ 2 + 15.1214 ^ 2) = 16.92m / s
The angle is:
x = atan (-15.1214 / 7.6) = -63.32 deg

Answer:
y = 11.68 m
x = 23.4536 m
16.92m / s
-63.32 deg