Question

Find the radius of the given circle with the center at (-2,1) and a point on the circle at (0,3).​

Answer 1

The radius of the given circle ( r ) = 2√2

Explanation:

Step(i):-

Given that the center of the circle C = ( -2,1)

Given a point on the circle P = (0,3)

The distance between the center and point is called the radius of the circle

CP = radius of the circle

Step(ii):-

`CP = \sqrt{x_(2) - x_(1))^(2) +(y_(2) -y_(1) )^(2) }`

`CP = \sqrt{(0 - (-2))^(2) +(3-1)^(2) } \\CP = √(4+4)`

CP = √8 =
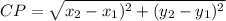
`√(4 X 2) = 2√(2)`

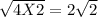
Final answer:-

The radius of the given circle ( r ) = 2√2