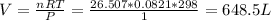Question

URGENT HELP NEEDED

When 100 liters of butane, C4h10, are reacted at SP (standard Pressure) and 25°C. How many liters of oxygen are required under the same conditions?
2 C₄H₁₀(g) + 13 O₂(g) ⇄ 8 CO₂(g) + 10H₂O(l)

Answer 1

Volume of O2 = 649 L

Step-by-step explanation:

Given data:

Volume of butane, V = 100 L

Temperature , T = 25 C = 25 + 273 = 298 K

Standard Pressure, P = 1 atm

Step 1: Calculate the moles of butane using ideal gas equation

`PV = nRT`

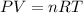
where n = number of moles, R = 0.0821 Latm/mol-K

`n = (PV)/(RT) = (1*100)/(0.0821*298) = 4.087 moles`

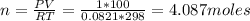
Step 2: Calculate moles of O2 required from Reaction stoichiometry

2 C₄H₁₀(g) + 13 O₂(g) ⇄ 8 CO₂(g) + 10H₂O(l)

Based on the stoichiometry:

2 moles of butane reacts with 13 moles of O2

Therefore, 4.087 moles of butane will react with:

`(4.078 butane*13 O2)/(2 butane ) = 26.507 moles O2`

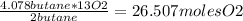
Step 3: Calculate the volume of O2 required

Again from ideal gas equation:

`V = (nRT)/(P) = (26.507*0.0821*298)/(1) = 648.5 L`

Answer 2

the balanced equation for the reaction is as follows
2C₄H₁₀ + 13O₂ ---> 8 CO₂ + 10H₂O
stoichiometry of C₄H₁₀ to O₂ is 2:13
stoichiometry applies to the molar ratio of reactants and products. Avagadros law states that volume of gas is directly proportional to number of moles of gas when pressure and temperature are constant.
Therefore volume ratio of reactants is equal to molar ratio, volume ratio of C₄H₁₀ to O₂ is 2:13
2 L of C₄H₁₀ reacts with 13 L of O₂
then 100 L of C₄H₁₀ reacts with 13/2 x 100 = 650 L
therefore 650 L of O₂ are required