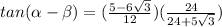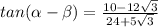Question

How is this solved using trig identities (sum/difference)?

Answer 1

FIRST PART
We need to find sin α, cos α, and cos β, tan β
α and β is located on third quadrant, sin α, cos α, and sin β, cos β are negative

Determine ratio of ∠α
Use the help of right triangle figure to find the ratio
tan α = 5/12
side in front of the angle/ side adjacent to the angle = 5/12
Draw the figure, see image attached

Using pythagorean theorem, we find the length of the hypotenuse is 13
sin α = side in front of the angle / hypotenuse
sin α = -12/13

cos α = side adjacent to the angle / hypotenuse
cos α = -5/13

Determine ratio of ∠β
sin β = -1/2
sin β = sin 210° (third quadrant)
β = 210°


`cos \beta = -(1)/(2) √(3)`


`tan \beta= (1)/(3) √(3)`

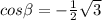
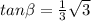SECOND PART
Solve the questions
Find sin (α + β)
sin (α + β) = sin α cos β + cos α sin β

`sin( \alpha + \beta )=(- (12)/(13) )( -(1)/(2) √(3))+( -(5)/(13) )( -(1)/(2) )`

`sin( \alpha + \beta )=((12)/(26)√(3))+( (5)/(26) )`

`sin( \alpha + \beta )=((5+12√(3))/(26))`

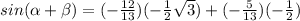
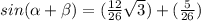
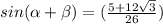
Find cos (α - β)
cos (α - β) = cos α cos β + sin α sin β

`cos( \alpha + \beta )=(- (5)/(13) )( -(1)/(2) √(3))+( -(12)/(13) )( -(1)/(2) )`

`cos( \alpha + \beta )=((5)/(26) √(3))+( (12)/(26) )`

`cos( \alpha + \beta )=((5√(3)+12)/(26) )`

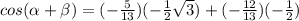
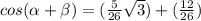
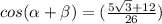
Find tan (α - β)

`tan( \alpha - \beta )= ( tan \alpha-tan \beta )/(1+tan \alpha tan \beta )`

`tan( \alpha - \beta )= ( (5)/(12) - (1)/(2) √(3) )/(1+((5)/(12)) ( (1)/(2) √(3)))`

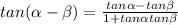
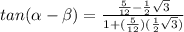
Simplify the denominator

`tan( \alpha - \beta )= ( (5)/(12) - (1)/(2) √(3) )/(1+((5√(3))/(24)))`

`tan( \alpha - \beta )= ( (5)/(12) - (1)/(2) √(3) )/( (24+5√(3))/(24) )`

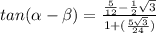
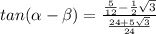
Simplify the numerator

`tan( \alpha - \beta )= ( (5)/(12) - (6)/(12) √(3) )/( (24+5√(3))/(24) )`

`tan( \alpha - \beta )= ( (5-6√(3))/(12) )/( (24+5√(3))/(24) )`

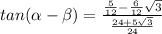
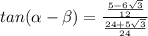
Simplify the fraction

`tan( \alpha - \beta )= ((5-6√(3))/(12) })({ (24)/(24+5√(3)))`

`tan( \alpha - \beta )= (10-12√(3) )/( 24+5√(3))`