1)
cos(α) > 0, is just another way to say cos(α) is positive, and therefore, the adjacent side is positive then.
now, on -4/5, keep in mind that the hypotenuse is just a radius unit, and therefore is never negative, so in -4/5, the negative has to be the -4.

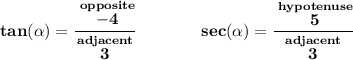
2)


hmm the sec(x) < 0, is just another way to say sec(x) is negative, and since the cosine is the reciprocal of the secant, then the cosine is also negative. Now in the fraction -3/2, which is the negative? since it could be -3/2 or 3/-2, well, anyhow, is the -3, because is the adjacent side, which is used by the cosine, that we know is negative.