Question

The function f(x)=2^x and g(x)=f(x+k). If k=-5,what can be concluded about the graph of g(x)?

Answer 1

`\bf ~~~~~~~~~~~~\textit{function transformations} \\\\\\ % templates f(x)= A( Bx+ C)+ D \\\\ ~~~~y= A( Bx+ C)+ D \\\\ f(x)= A√( Bx+ C)+ D \\\\ f(x)= A(\mathbb{R})^( Bx+ C)+ D \\\\ f(x)= A sin\left( B x+ C \right)+ D \\\\ --------------------`


`\bf \bullet \textit{ stretches or shrinks horizontally by } A\cdot B\\\\ \bullet \textit{ flips it upside-down if } A\textit{ is negative}\\ ~~~~~~\textit{reflection over the x-axis} \\\\ \bullet \textit{ flips it sideways if } B\textit{ is negative}\\ ~~~~~~\textit{reflection over the y-axis} \\\\ \bullet \textit{ horizontal shift by }( C)/( B)\\ ~~~~~~if\ ( C)/( B)\textit{ is negative, to the right}`


`\bf ~~~~~~if\ ( C)/( B)\textit{ is positive, to the left}\\\\ \bullet \textit{ vertical shift by } D\\ ~~~~~~if\ D\textit{ is negative, downwards}\\\\ ~~~~~~if\ D\textit{ is positive, upwards}\\\\ \bullet \textit{ period of }(2\pi )/( B)`

with that template in mind


`\bf f(x)=2^x\qquad \begin{cases} g(x)=f(x+k)&k=5\\ \qquad\quad f(x+5)\\ \qquad \quad 2^(x+5) \end{cases}`

notice, in g(x)

B = 1, no change from parent

C= +2

Answer 2

The graph of g(x) is obtained by translating the function of f(x) by shifting the graph to right by 5 units

Explanation:

The function f(x) is given to be :

`f(x)=2^x`

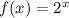
Also, The function g(x) is given to be : g(x) = f(x + k)

Now, The value of k = -5

So, The function g(x) becomes g(x) = f(x - 5)

The function f(x - 5) shows that the function is translated by shifting the graph of f(x) to right by 5 units.

Thus, The graph of g(x) is obtained by translating the function of f(x) by shifting the graph to right by 5 units