Question

For the line segment whose end points are R(1,2) and S(6,7) find the y value for the point located 3/4 the distance from R to S.

A) 4.25
B) 4.75
C) 5.25
D) 5.75

Answer 1

Answer: The answer is C) 5.25

Answer 2

so, let's see, the point say P, is 3/4 of the way from R to S, namely, if we split the segment RS into 4 pieces, from R to P, or RP will take 3 of those quarters, and from P to S, or PS, will take one of those quarters, check the picture below.

so the RP section is at a ratio of 3, whilst the PS section is at a ratio of 1.


`\bf ~~~~~~~~~~~~\textit{internal division of a line segment} \\\\\\ R(1,2)\qquad S(6,7)\qquad \qquad 3:1 \\\\\\ \cfrac{R\underline{P}}{\underline{P} S} = \cfrac{3}{1}\implies \cfrac{R}{S} = \cfrac{3}{1}\implies 1R=3S\implies 1(1,2)=3(6,7)\\\\ -------------------------------`


`\bf { P=\left(\cfrac{\textit{sum of`

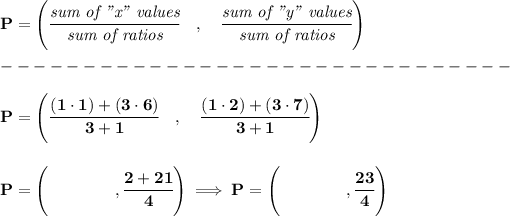
and that's the y-coordinate for the point P.