Question

A pendulum with a mass of 1 kg is released from a height of 1.5 cm above the height of its resting position. How fast will the pendulum be moving when it passes through the lowest point of its swing?

Answer 1

v = 0.54 m/s

Step-by-step explanation:

The Principle Of Conservation Of Mechanical Energy

In the absence of friction, the total mechanical energy is conserved. That means that

Em=U+K is constant, being U the potential energy and K the kinetic energy

U=mgh

`\displaystyle K=(mv^2)/(2)`

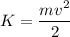
When the mass (m=1 kg) of the pendulum is at the top of the path at a height of h=1.5 cm=0.015 m, its kinetic energy is 0 and its potential energy is:

U=1 * 9.8 * 0.015 = 0.147 J

That potential energy is completely transformed into kinetic energy at the bottom of the swing. The speed can be calculated by solving for v:

`\displaystyle (mv^2)/(2)=0.147`

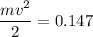
Multiplying by 2 and dividing by m:

`\displaystyle v^2=(2K)/(m)`

`\displaystyle v^2=(2*0.147)/(1)=0.294`

`v=√(0.294)`

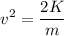
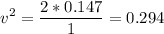
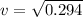
v = 0.54 m/s