Question

A bank manager wishes to provide prompt service for customers at the bank's drive-up window. the bank currently can serve up to 10 customers per 15-minute period without significant delay. the average arrival rate is 7 customers per 15-minute period. let x denote the number of customers arriving per 15-minute period. assuming x has a poisson distribution: (a) find the probability that 10 customers will arrive in a particular 15-minute period. (round your answer to 4 decimal places.) probability (b) find the probability that 10 or fewer customers will arrive in a particular 15-minute period. (do not round intermediate calculations for calculating probability. round your answer to 4 decimal places.) probability (c) find the probability that there will be a significant delay at the drive-up window. that is, find the probability that more than 10 customers will arrive during a particular 15-minute period. (do not round intermediate calculations for calculating probability. round your answer to 4 decimal places.) probability

Answer 1

The Poisson distribution with mean λ has

`P(K=k)=(\lambda ^k e^(-\lambda))/(k!)`

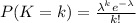
Here
time period = 15 minutes
λ =7

(a) k=10 customers arrive within a time period (15 minutes)
Find P(K=10)

`P(K=k)=(\lambda ^k e^(-\lambda))/(k!)`

`=(7 ^(10) e^(-7))/(10!)`

`=0.0709833`

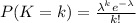
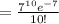
(b) Find P(K<=10)
P(K<=10)
=
`\sum_(i=0)^(10) P(K=i)=(\lambda ^i e^(-\lambda))/(i!)`
=0.000912+0.006383+0.022341+0.052129+0.091226+0.127717+0.149003+0.149003+0.130377+0.101405+0.070983
=0.901479

(c) Find P(K>10)
P(K>10)
=1-P(K<=10)
=1-0.901479
=0.098521