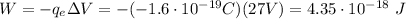Question

To form a hydrogen atom, a proton is fixed at a point and an electron is brought from far away to a distance of 0.529 ✕ 10−10 m, the average distance between proton and electron in a hydrogen atom. how much work is done by the electric field (in j)?

Answer 1

1) First of all, let's calculate the potential difference between the initial point (infinite) and the final point (d=0.529x10-10 m) of the electron.
This is given by:

`\Delta V =- \int\limits^(d)_(\infty) {E} \, dr`
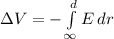
Where E is the electric field generated by the proton, which is

`E=k_e (q)/(r^2)`
where
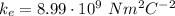
`k_e=8.99\cdot10^9~Nm^2C^(-2)` is the Coulomb constant and
`q=1.6\cdot10^(-19)~C` is the proton charge.
Replacing the electric field formula inside the integral, we obtain

`\Delta V =- \int\limits^(d)_(\infty) {k_e (q)/(r^2) } \, dr = k_e (q)/(d)= 27~V`

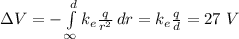
2) Then, we can calculate the work done by the electric field to move the electron (charge
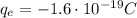
`q_e=-1.6\cdot10^(-19)C`) through this
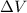
`\Delta V`. The work is given by

`W=-q_e \Delta V = - (-1.6\cdot10^(-19)C) (27V)=4.35\cdot10^(-18)~J`