Question

The waiting times between a subway departure schedule and the arrival of a passenger are uniformly distributed between 00 and 77 minutes. find the probability that a randomly selected passenger has a waiting time greater than greater than 3.253.25 minutes.

Answer 1

Uniform distribution between 0 and 7 minutes.
Need to know probability of waiting greater than 3.25 minutes.

P(T>3.25) = (7-3.25)/(7-0) = 0.536

Answer: the probability that waiting time exceeds 3.25 minutes is 0.536

Answer 2

Answer: 0.5357

Explanation:

If a continuous random variable x is distributed uniformly in interval [a,b] , then the probability density function is given by :-

`f(x)=(1)/(b-a)`

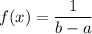
Given : The waiting times between a subway departure schedule and the arrival of a passenger are uniformly distributed between 0 and 7 minutes.

Probability density function=
`f(x)=(1)/(7-0)=(1)/(7)`

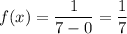
Now, the probability that a randomly selected passenger has a waiting time greater than greater than 3.253.25 minutes :-

`\int^(7)_(3.25)\ f(x)\ dx\\\\= (1)/(7)\int^(7)_(3.25)\ dx\\\\  (1)/(7)[x]^(7)_(3.25)\\\\=(1)/(7)[7-3.25]=(3.75)/(7)=0.535714285\approx0.5357`

Hence, the required probability = 0.5357