Question

Identify the conic section represented by the equation:
x2 + 2x + 2y2 – 12y + 11 = 0
2

Answer 1

Equation of the Ellipse

`((x+1)^(2) )/(8) + ((y-3)^(2) )/(4) = 1`

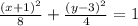
Explanation:

Step(i):-

Given that the equation

x² + 2 x + 2y² - 12 y +11 = 0

⇒ x² + 2 x + 1 - 1 + 2(y² - 6 y )+ 11 = 0

x² + 2 x + 1 - 1 + 2(y² - 2(3) y+9-9 )+ 11 = 0

⇒ x² + 2 x + 1 - 1 + 2(y² - 2(3 y ) + 3²- 3² ) + 11 = 0

By using (a +b)² = a² + 2 a b + b²

(a -b)² = a² - 2 a b + b²

Step(ii):-

x² + 2 x + 1 - 1 + 2(y² - 2(3 y ) + 3²- 3² ) + 11 = 0

⇒ ( x+1)² +2( y-3 )² - 1 - 2(9) +11 =0

⇒ ( x+1)² +2( y-3 )² - 8 =0

( x+1)² +2( y-3 )² = 8

Dividing '8' on both sides , we get

`((x+1)^(2) )/(8) + (2(y-3)^(2) )/(8) = 1`

`((x+1)^(2) )/(8) + ((y-3)^(2) )/(4) = 1`

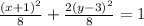
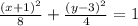
This equation represents the Ellipse