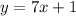ANSWER
The required equation is
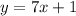
Step-by-step explanation
Let the equation of the line be
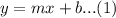
where
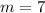
is the slope of the line. We substitute this value of the slope into the equation (1) to obtain,
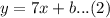
Since the point (1,8) lies on the line, it must satisfy this equation.
We substitute the x and y value of the point into the equation(2) to get,
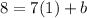
This simplifies to give us,
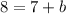
We solve for b to get,
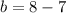
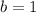
We substitute the value of b back into equation (2) to get