Question

The functions f(x)=−
`(3)/(4)`x+2
`(1)/(4)` and g(x)=(12)x+1 are shown in the graph.

What are the solutions to −
`(3)/(4)`x+2
`(1)/(4)`=(
`(1)/(2)`)x+1?

Select each correct answer.


A)−1

B)0

C)1

D)2

E) 3

[Graph is included in the photo]

Answer 1

Answer: options A) x = -1 and C) x = 1

Step-by-step explanation:

The graph show that the two functions intersect at x = - 1 and x = 1, so those are the solutions to the equality given. That is the options A) and C).

Note that the first function,
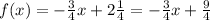
`f(x)=- (3)/(4) x+2 (1)/(4) = - (3)/(4) x+ (9)/(4)` is the the straight line.

The function g(x) is
`( (1)/(2)) ^x+1`

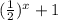
When you replace the value of x = -1 you get:

f(-1) = - (3/4) (-1) + 9/4 = 3/4 + 9/4 = 12 / 4 = 3

g(-1) = (1/2)^(-1) + 1 = 2 + 1 = 3

So, f(-1) = g(-1).

When you replace x = 1 you get:

f(1) = -(3/4)(1) + 9/4 = -3/4 + 9/4 = 6/4 = 3/2

g(1) = (1/2)^1 + 1 = 1/2 + 1 = 3/2

So, f(1) = g(1).

And in that way you have shown analiticaly that x = -1 and x = 1 are both solutions of f(x) = g(x).