Piecewise function can be explained as a set of subfunctions (each subfunction applied to an interval). Here we can observe a piecewise function that is composed of three sub functions.
-The first subfunction: between 0 and 3 (open interval in 3) there is a quadratic function, we can obtain it from the general form of the quadratic function when it has a vertex on (0,0) which is:
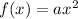
 will be a positive value if the parabola is opening upward and negative if it is opneing downward. This one opens upward so it is positive and it will be =1 because when we make
will be a positive value if the parabola is opening upward and negative if it is opneing downward. This one opens upward so it is positive and it will be =1 because when we make
 on the graph corresponds to
on the graph corresponds to
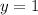 so:
so:
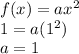
Our subfunction if
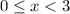 is
is
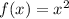
-the second and third subfunctions: both are straight lines defined each in an interval. The first between 3 and 6 (open interval in 3) and the second between 6 and 10. To build this two functions we need to understand the general form of the line function:
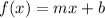
where m is the slope of the line and b is the y intercept.
we calculate first m and b for both lines with the m and b equation (we must take two coordintates of each line (
 ):
):

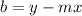
First line (4,6),(5,5)
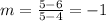
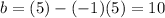
Second line (8,7),(10,10)

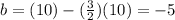
Now we can build both the equations:
First Lline (
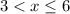 )
)
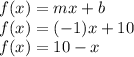
Second Line(
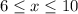 ):
):
