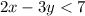Question

Which inequality matches the graph? X, Y graph. X range is negative 10 to 10, and Y range is negative 10 to 10. Dashed line on graph has positive slope and runs through negative 10, negative 9 and negative 1, negative 3 and 8, 3. Above line is shaded. −2x + 3y > 7 2x − 3y < 7 −3x + 2y ≥ 7 3x − 2y ≤ 7

Answer 1

The Answer is A. −2x + 3y > 7

Hope This Helps!

Answer 2

The inequality that matches the graph is:

`2x-3y<7`

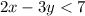
Explanation:

It is given that the line is a dashed line.

This means that the inequality is strict.

Also, the dashed line passes through (-10,-9) and (-1,-3) and (8,3)

Using two point formula we may find the equation of the line.

i.e. any line passing through two points (a,b) and (c,d) is calculated by using the equation:

`y-b=(d-b)/(c-a)* (x-a)`

Here (a,b)=(-10,-9) and (c,d)=(-1,-3)

The equation of line is:

`y-(-9)=(-3-(-9))/(-1-(-10))* (x-(-10))\\\\i.e.\\\\y+9=(-3+9)/(-1+10)* (x+10)\\\\i.e.\\\\y+9=(6)/(9)* (x+10)\\\\i.e.\\\\y+9=(2)/(3)* (x+10)\\\\3(y+9)=2* (x+10)\\\\3y+27=2x+20\\\\i.e.\\\\2x-3y=27-20\\\\i.e.\\\\2x-3y=7`

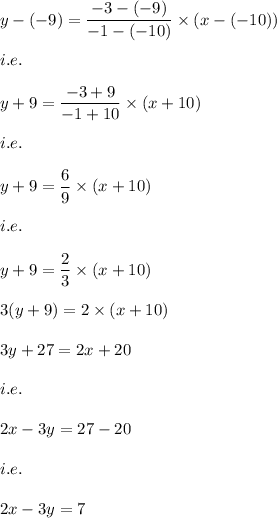
Also, the shaded region is above the line.

Hence, the inequality is:

`2x-3y<7`