Question

Evaluate the integral. (use c for the constant of integration.) 8 sin2(x) cos3(x) dx

Answer 1

Important formula we will use.
First formula
2 cos α sin β = sin (α + β) - sin (α - β)
Second formula
∫ sin x dx = - cos x + c

We should change the trigonometry expression from multiplication into addition. Use the first formula above
∫ 8 sin (2x) cos (3x) dx
= ∫ 4 ( 2 sin (2x) cos (3x) dx)
= 4 ∫ 2 cos (3x) sin (2x) dx
= 4 ∫ sin (3x + 2x) - sin (3x - 2x) dx
= 4 ∫ sin 5x - sin x dx

After changing into addition, solve the integration. Use the second formula.
= 4 ∫ sin 5x - sin x dx

`= 4(- (1)/(5) cos5x-cosx)+c`

`= - (4)/(5) cos5x-4cosx+c`
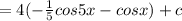
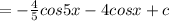
This is the answer.