Question

The average time a boulder high varsity lacrosse player plays in a game is 32 minutes with a standard deviation of 9 minutes. nolan's playing time in last week's game against fairview was 44 minutes. (a) calculate the z-score for nolan's playing time against fairview. (round your answer to 2 decimal places.) nolan's standardized z-score 1.33 (b) by the empirical rule, was nolan's playing time unusual when compared to the typical playing time

Answer 1

(a) The z-score is calculated by subtracting the population mean from the x value and dividing this difference by the standard deviation.

If Nolan played for 44 minutes in last week's game against fairview, then his z-score would be:


`z= (44-32)/(9)=(12)/(9)=1.33`

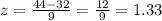ANSWER: The z-score for Nolan's playing time against fairview is 1.33.

(b) Since the z-score for Nolan's playing time against fairview is 1.33, then we know that his playing time is 1.33 standard deviations from the mean. If you compare this to the fact that 95% of all data fall within two standard deviations from the mean (empirical rule), then Nolan's playing time would not be unusual compared to the typical playing time.