Question

What is the solution of log2x+7 27= 3

Answer 1

`log_(2x+7) 27=3`
(2x+7)^3=27

`2x+7= \sqrt[3]{27}`
2x+7=3
2x=-4
x=-2

Answer 2

`x=-2`

Explanation:

`log_(2x+7)(27)= 3`

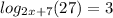
We need to find the value of x

WE write the given log equation in exponential form'

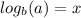`log_b(a)=x` can be written as
`b^x=a`

Using this we convert log to exponential form

`log_(2x+7)(27)= 3`

`(2x+7)^3= 27`

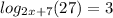
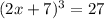
27 can be written as 3^3

`(2x+7)^3= 3^3`

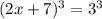
Both sides have exponent 3. To remove exponent 3 we take cube root on both sides.

`2x+7=3`

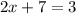
Subtract 7 on both sides

`2x=-4`

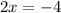
Divide both sides by 2

`x=-2`