Question

Cobalt-60 has an annual decay rate of about 13%.

How many grams of a 300 g sample will remain after 20 years?

Round the answer to two decimal places.


A. 0.06 g

B. 9.38 g

C. 18.51 g

D. 37.50 g

Answer 1

the answer will be c

Answer 2

Option: C is the correct answer.

C. 18.51 g

Explanation:

The situation of this problem can be modeled with the help of the exponential decay function :

i.e. any component if it has a initial amount as a units and is decaying at a rate of r% then the amount after t years is given by:

`n(t)=a(1-(r)/(100))^t`

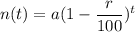
Here we have:

r=13%

and a=300 g

and t=20 years

Hence, we have

`n(20)=300\cdot (1-(13)/(100))^(20)\\\\i.e.\\\\n(20)=300\cdot (1-0.13)^(20)\\\\i.e.\\\\n(20)=300\cdot (0.87)^(20)\\\\n(20)=300\cdot 0.061714\\\\i.e.\\\\n(20)=18.5142\ g`

The amount that will be left after 20 years is: 18.51 g