Question

Which expression will equal a rational product even though it is multiplying an irrational number times another irrational number?

Answer 1

A. The square of an irrational number \sqrt(11)=\sqrt(11)*\sqrt(11)=\sqrt(11^2)=11, which is a rational number. However, in B, C, and D, the two pair of rational numbers cannot multiply to become a rational number.

Answer 2

Answer: option A.
`√(11) . √(11)`

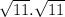
Justification:

By definition the product of the square root of a number times itself is the same number.

This is:
`√(n) . √(n) = n`


Because:
`√(n) . √(n) =( √(n))^2 = n`


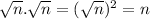
Therefore, for the case given:
`√(11) . √(11) = 11`

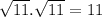
And you have proved that the product of the two irrational numbers, √11, is a ratonal number, 11.

On the other hand, the other products, B, C, and D do not yield to a rational number. The result of the products shown on B, C, and D are irrational.