Answer: The correct option is (A) 125 : 64.
Step-by-step explanation: Given that the ratio of the heights and radii of two similar cylinders is 5 : 4.
We are to find the ratio for the volumes of the two cylinders.
We know that the volume of a cylinder with radius r units and height h units is given by
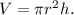
Let r, r' be the radii and h, h' be the heights of the two similar cylinders.
Then, the volumes of the two cylinders will be
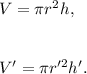
According to the given information, we have

Therefore, we get

Thus, the required ratio of the volumes of the two cylinders is 125 : 64.
Option (A) is CORRECT.