Question

A ladder is leaning against a wall and makes an 82° angle of elevation with the ground.

Part A: If the base of the ladder is 4 feet from the wall, then how long is the ladder? Round to the nearest tenth.
Part B: Determine how high up the wall does the ladder reach.

Answer 1

check the picture below.

make sure your calculator is in Degree mode.

Answer 2

part A : the length of the ladder is 28.7 feet

part B: the height of the wall the ladder reaches is 28.5 feet

Explanation:

The A part of the question states that we should find how long the ladder is.

The base of the ladder is 4 feet from the wall, this implies that the adjacent is 4, the length of the ladder which we are ask to find is the hypotenuse, let the hypotenuse by x.

We are going to use the trigonometric ratio;

SOH CAH TOA

sin Ф = opposite/hypotenuse

cosФ = adjacent / hypotenuse

tan Ф = opposite/adjacent

From what we have, which are; Ф=82 adjacent=4 hypotenuse=x

Then the best formula to use is;

cosФ = adjacent / hypotenuse

Lets proceed to insert our values into the formula;

cos 82 =
`(4)/(x)`

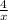
cross-multiply

xcos82 = 4

Divide both-side of the equation by cos 82

`(xcos82)/(cos82)` =
`(4)/(cos 82)`

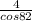
x = 28.741

x≈28.7 to the nearest tenth.

Therefore the length of the ladder is 28.7 feet

Part B says we should determine how high up the wall does the ladder reach.

the height of the wall is the opposite, let the opposite be y.

In dealing with this part of the question; Ф=82, adjacent = 4 feet, opposite=y

Then the best formular to use is;

tan Ф = opposite/adjacent

Lets now proceed to insert our values into formula;

tan 82 =
`(y)/(4)`

cross-multiply

y = 4tan82

y = 28.461

y≈28.5 to the nearest tenth.

Therefore the height of the wall the ladder reaches is 28.5 feet