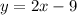Question

write the equation for the line that is perpendicular to given line that passes through the given point -3x-6y=17; (6,3)

Answer 1

`y=2x-9`

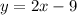
Explanation:

you have the line

`-3x-6y=17`

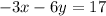
clearing for y:

`-6y=17+3x\\y=(17)/(-6) +(3)/(-6) x\\y=-(1)/(2) x-(17)/(6)`

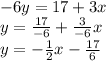
we have an equation of the form

`y=mx+b`

the number that accompanies the x is the slope, and the number alone is the intercept with the y-axis

the slope m is:

`m=-(1)/(2)`

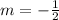
i will call the slope of the new line
`m_(2)`

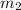
so for two perpendiculares lines we must have:
`m*m_(2)=-1`

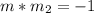
and from this we can find the new slope:

`m_(2)=(-1)/(m) \\\\m_(2)=(-1)/((-1)/(2) ) \\m_(2)=2`

the new slope is 2,

so far we have that the new line is:

`y=2x+b`

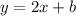
so now we have to find the intercept with the y axis (
`b`) of the new line, since it passes trough (6,3) ---> x = 6 when y = 3

substituting these x and y values in
`y=2x+b`:

`3=2(6)+b\\3=12+b\\b=3-12\\b=-9`

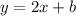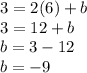
and finally, the equation of the new line that is perpendicular to the original line is:

`y=2x-9`