Answer:
(D)
Explanation:
The given equation is:
![\sqrt[3]{x^2-12}=\sqrt[3]{4x}](https://img.qammunity.org/2019/formulas/mathematics/high-school/mffj5q1epi5rvbgo4xipzq46sf6dgxeo9t.png)
Cubing on both the sides, we get
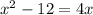
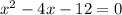
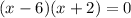
therefore, the solutions are:
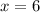 and
and

Substitute x=6 in the given equation, we have
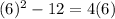
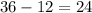
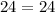
which is true, thus x=6 is a true solution.
Put x=-2 in the given equation, we have
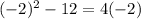
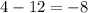
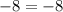
which is true, thus x=-2 is a true solution.
Therefore, Both x = –2 and x = 6 are true solutions.