Answer: The correct number of balls is (b) 4.
Step-by-step explanation: Given that a single winner is to be chosen in a random draw designed for 210 participants. Also, there is an equal probability of winning for each participant.
We are using 10 balls, numbered through 0 to 9. We are to find the number of balls which needs to be picked up, regardless of order, so that each of the 210 participants can be assigned a unique set of numbers.
Let 'r' represents the number of balls to be picked up.
Since we are choosing from 10 balls, so we must have
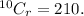
The value of 'r' can be any one of 0, 1, 2, . . , 10.
Now,
if r = 1, then
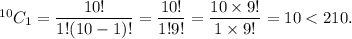
If r = 2, then
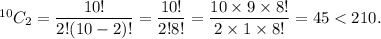
If r = 3, then
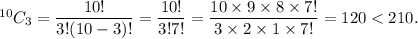
If r = 4, then
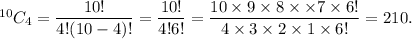
Therefore, we need to pick 4 balls so that each participant can be assigned a unique set of numbers.
Thus, (b) is the correct option.